SSLL103を参考に線形座屈解析をしてみました。
線形座屈解析は
$$ (K+\lambda K_{g})x = 0 $$
ここで
$$K:剛性マトリックス\\
K_{g}:形状剛性マトリックス\\
\lambda :固有値$$
を解くことです.解析の手順は次の通りですね。
- 静解析を行う
- 静解析の結果を使って、剛性マトリックスと形状剛性マトリックスを作成
- 固有値解析
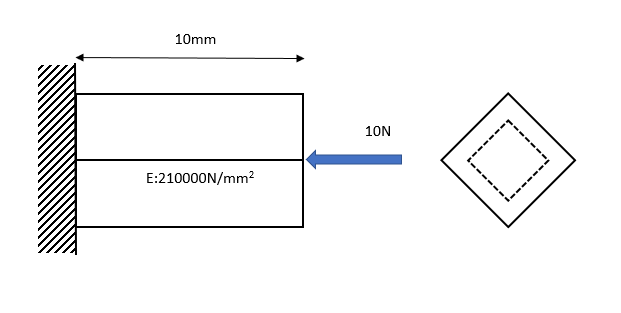
解析対象のモデルは次のとおり。はりの断面形状は、こちらのものです。
DEBUT(identifier=u'0:1',
LANG='EN')
mesh = LIRE_MAILLAGE(identifier=u'1:1',
FORMAT='MED',
UNITE=3)
meshsect = LIRE_MAILLAGE(identifier=u'2:1',
FORMAT='MED',
UNITE=20)
model = AFFE_MODELE(identifier=u'3:1',
AFFE=_F(MODELISATION=('POU_D_T', ),
PHENOMENE='MECANIQUE',
TOUT='OUI'),
MAILLAGE=mesh)
tsect = MACR_CARA_POUTRE(identifier=u'4:1',
GROUP_MA_BORD=('border', ),
GROUP_MA_INTE=('inn', ),
GROUP_NO=('origin', ),
MAILLAGE=meshsect,
NOM='1',
TABLE_CARA='OUI')
elemprop = AFFE_CARA_ELEM(identifier=u'5:1',
MODELE=model,
ORIENTATION=_F(CARA='VECT_Y',
GROUP_MA=('beam', ),
VALE=(0.0, 1.0, 0.0)),
POUTRE=_F(GROUP_MA=('beam', ),
NOM_SEC='1',
SECTION='GENERALE',
TABLE_CARA=tsect,
VARI_SECT='CONSTANT'))
steel = DEFI_MATERIAU(identifier=u'6:1',
ELAS=_F(E=210000.0,
NU=0.3))
fieldma0 = AFFE_MATERIAU(identifier=u'7:1',
AFFE=_F(MATER=(steel, ),
TOUT='OUI'),
MAILLAGE=mesh,
MODELE=model)
load = AFFE_CHAR_MECA(identifier=u'8:1',
DDL_IMPO=_F(DRX=0.0,
DRY=0.0,
DRZ=0.0,
DX=0.0,
DY=0.0,
DZ=0.0,
GROUP_NO=('fix', )),
FORCE_NODALE=_F(FZ=-10.0,
GROUP_NO=('load', )),
MODELE=model)
STAT1 = MECA_STATIQUE(identifier=u'9:1',
CARA_ELEM=elemprop,
CHAM_MATER=fieldma0,
EXCIT=_F(CHARGE=load),
MODELE=model)
SIGMA_1 = CREA_CHAMP(identifier=u'10:1',
NOM_CHAM='SIEF_ELGA',
NUME_ORDRE=1,
OPERATION='EXTR',
RESULTAT=STAT1,
TYPE_CHAM='ELGA_SIEF_R')
RIGEL = CALC_MATR_ELEM(identifier=u'11:1',
CARA_ELEM=elemprop,
CHAM_MATER=fieldma0,
CHARGE=(load, ),
MODELE=model,
OPTION='RIGI_MECA')
NU = NUME_DDL(identifier=u'12:1',
MATR_RIGI=(RIGEL, ))
RIGAS = ASSE_MATRICE(identifier=u'13:1',
MATR_ELEM=RIGEL,
NUME_DDL=NU)
RIGELG_1 = CALC_MATR_ELEM(identifier=u'14:1',
CARA_ELEM=elemprop,
MODELE=model,
OPTION='RIGI_GEOM',
SIEF_ELGA=SIGMA_1)
RIGASG_1 = ASSE_MATRICE(identifier=u'15:1',
MATR_ELEM=RIGELG_1,
NUME_DDL=NU)
MOD_1 = CALC_MODES(identifier=u'16:1',
MATR_RIGI=RIGAS,
MATR_RIGI_GEOM=RIGASG_1,
SOLVEUR_MODAL=_F(COEF_DIM_ESPACE=4),
TYPE_RESU='MODE_FLAMB')
IMPR_RESU(identifier=u'17:1',
FORMAT='MED',
RESU=_F(RESULTAT=MOD_1,
TOUT='OUI'),
UNITE=4)
IMPR_RESU(identifier=u'18:1',
FORMAT='RESULTAT',
RESU=_F(RESULTAT=MOD_1,
TOUT='OUI'),
UNITE=8)
FIN(identifier=u'19:1',
)
解析結果は
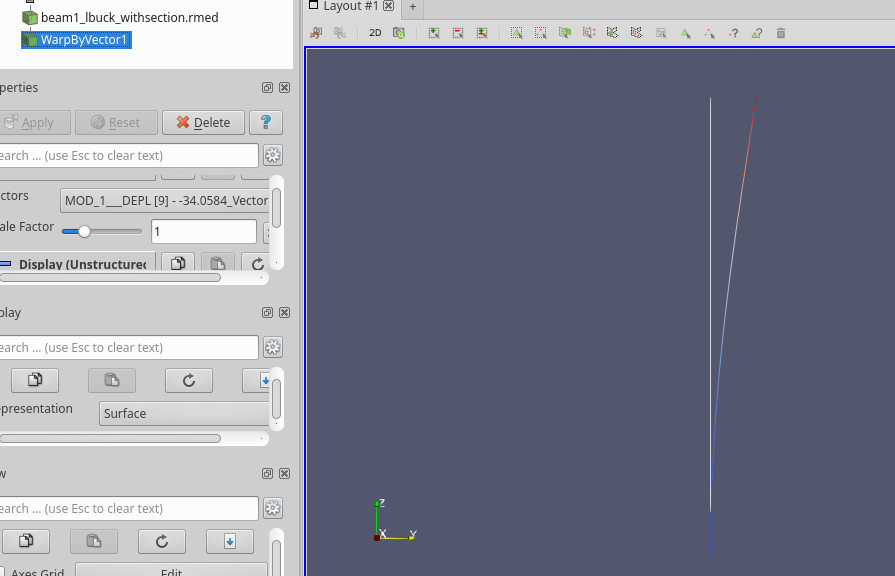
座屈荷重$P_{c}$は、$\lambda x F = 34.05×10=340.5N$でした。
Euler座屈の式から求めた値は
$P_{c}= n\frac{\pi^{2} E I}{L^{2}} $
$ = \frac{1}{4} \frac{\pi^{2} 210000 0.067333}{10^{2}}$
$ = 3.49×10^{2} N$
ですので、ほぼ一致しました。

コメント