INFO_MODEとCALC_MODESを使って線形座屈解析を行いました。
SDLS504AはI形鋼の座屈を扱っています。
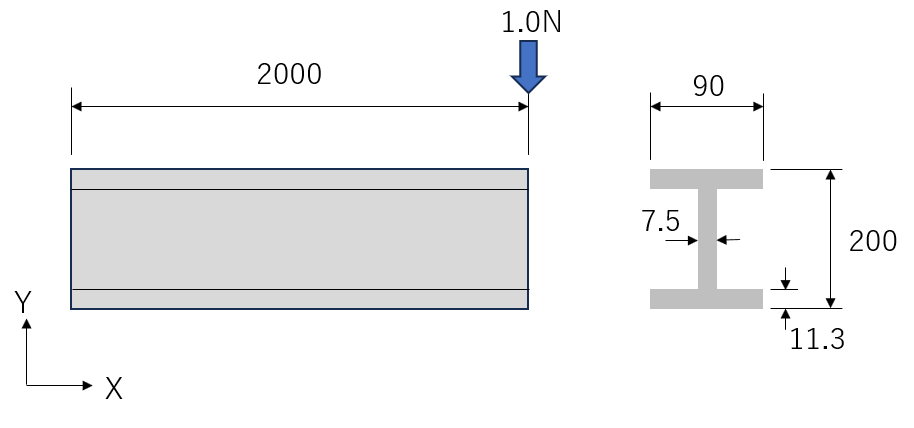
この手の解析で悩まされるのが、”負の固有値”です。商用ソフトでは下限値に0を設定して回避できるので、同じようなことができないかなと思って試してみました。
pythonによる処理をcommに加えるので、ASTKからCode asterを起動します。そのため次のように入力してastkを起動します。
$ singularity shell salome_meca-lgpl-2021.0.0-0-20210601-scibian-9.sif Singularity > astk
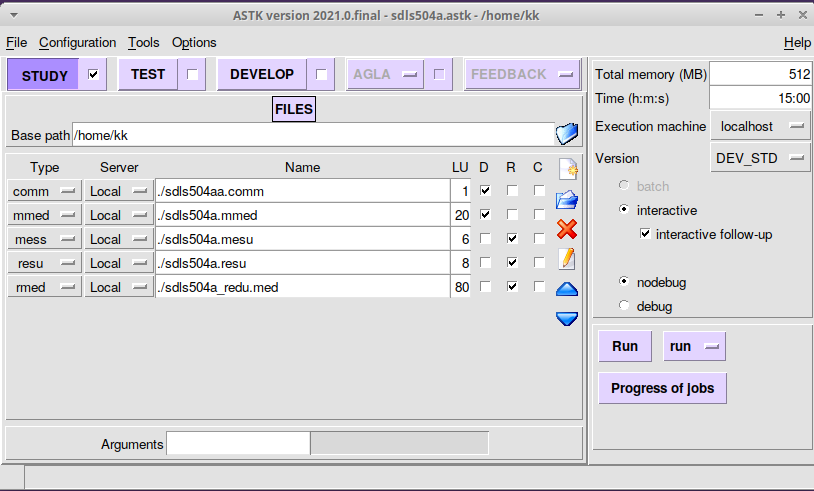
そして入力ファイルと出力ファイルを指定しました。
commファイルを次に示します。
DEBUT(PAR_LOT='NON', # pythonを使うので。
CODE=_F(NIV_PUB_WEB='INTERNET'),
INFO=2)
meshの読み込み。
MA = LIRE_MAILLAGE(FORMAT='MED',
UNITE=20)
読み込んだmeshを高次要素に変更します。
MAIL = CREA_MAILLAGE(MAILLAGE=MA,
MODI_MAILLE=_F(OPTION='TRIA6_7',
TOUT='OUI'))
MOEL = AFFE_MODELE(AFFE=_F(MODELISATION='COQUE_3D',
PHENOMENE='MECANIQUE',
TOUT='OUI'),
MAILLAGE=MAIL)
#---------------------------------------------------------------------
#CARACTERISTIQUES ELEMENTAIRES
#---------------------------------------------------------------------
CAEL = AFFE_CARA_ELEM(COQUE=(_F(A_CIS=5650.0,
EPAIS=0.0113,
GROUP_MA='SEMELLES'),
_F(ANGL_REP=(90.0, 0.0),
A_CIS=3750.0,
EPAIS=0.0075,
GROUP_MA='AME')),
MODELE=MOEL)
材料特性といて鋼のヤング率とポアソン比を設定し、meshに適用します。
#---------------------------------------------------------------------
#CARACTERISTIQUES MATERIAUX
#---------------------------------------------------------------------
MATERIAU = DEFI_MATERIAU(ELAS=_F(E=200000000000.0,
NU=0.3))
CHAM_MAT = AFFE_MATERIAU(AFFE=_F(MATER=MATERIAU,
TOUT='OUI'),
MAILLAGE=MAIL)
境界条件(拘束条件と荷重)を設定します。
#---------------------------------------------------------------------
#CHARGEMENTS
#---------------------------------------------------------------------
CON_LI = AFFE_CHAR_MECA(DDL_IMPO=_F(DRX=0.0,
DRY=0.0,
DRZ=0.0,
DX=0.0,
DY=0.0,
DZ=0.0,
GROUP_NO='ENCASTRE'),
MODELE=MOEL)
CHARGE = AFFE_CHAR_MECA(FORCE_NODALE=_F(FY=-1.0,
GROUP_NO='P'),
MODELE=MOEL)
線形解析を行います。
#PRE-ESTIMATIONS DU SPECTRE
#VALEURS ATTENDUES: 1, 3, 0 ET 5
#---------------------------------------------------------------------
#RESOLUTION
#---------------------------------------------------------------------
RES = MECA_STATIQUE(CARA_ELEM=CAEL,
CHAM_MATER=CHAM_MAT,
EXCIT=(_F(CHARGE=CON_LI),
_F(CHARGE=CHARGE)),
MODELE=MOEL,
SOLVEUR=_F(METHODE='MULT_FRONT'))
#REUTILISATION DU CALCUL DU NBRE DE CHARGES CRITIQUES D'INFO_MODECOMPARAISON AVEC LE #CALCUL COMPLET STANDARD (OPTION='BANDE') #CALCUL OPTION 'PLUS_PETITE'
座屈解析の準備をします。
SIGMA = CREA_CHAMP(NOM_CHAM='SIEF_ELGA',
OPERATION='EXTR',
RESULTAT=RES,
TYPE_CHAM='ELGA_SIEF_R',
TYPE_MAXI='MINI',
TYPE_RESU='VALE')
MEL_RI_G = CALC_MATR_ELEM(CARA_ELEM=CAEL,
MODELE=MOEL,
OPTION='RIGI_GEOM',
SIEF_ELGA=SIGMA)
MEL_RI_M = CALC_MATR_ELEM(CARA_ELEM=CAEL,
CHAM_MATER=CHAM_MAT,
CHARGE=(CHARGE, CON_LI),
MODELE=MOEL,
OPTION='RIGI_MECA')
NUM = NUME_DDL(MATR_RIGI=MEL_RI_M)
MAS_RI_M = ASSE_MATRICE(MATR_ELEM=MEL_RI_M,
NUME_DDL=NUM)
MAS_RI_G = ASSE_MATRICE(MATR_ELEM=MEL_RI_G,
NUME_DDL=NUM)
固有値を検出する範囲の区切りの値を設定します。
bands=[-1100000.0, -100000.0, 0.0, 500000.0, 1000000.0]
各区間の間に固有値が何個存在するのかを調べます。
今回は、-1100000から-100000、-100000から0、0から500000、500000から1000000の4区間です。
NBMOD1 = INFO_MODE(CHAR_CRIT= bands,
COMPTAGE=_F(METHODE='STURM'),
MATR_RIGI=MAS_RI_M,
MATR_RIGI_GEOM=MAS_RI_G,
SOLVEUR=_F(METHODE='MUMPS'),
TYPE_MODE='MODE_FLAMB')
NBMOD1から結果を取り出します。
nbmod = NBMOD1.EXTR_TABLE()
print('NBMOD ',nbmod.values())
各区間に存在する固有値の個数を取り出します。(NB_MODEで収納されています。)
nb_mode = nbmod.values()['NB_MODE']
各区間の下限と上限を取り出します。
cr_min = nbmod.values()['CHAR_CRIT_MIN']
cr_max = nbmod.values()['CHAR_CRIT_MAX']
print('NBMOD ',nb_mode) # これは確認のための出力です
座屈ですので0以上で一番小さな固有値を求めます。区間ごとに固有値の数を確認してから計算します。indentに注意しましょう。
for i in range(2,len(nb_mode)):
if nb_mode[i] > 0:
RESULT0 = CALC_MODES(CALC_CHAR_CRIT=_F(CHAR_CRIT=(cr_min[i], cr_max[i]),
TABLE_CHAR_CRIT=NBMOD1),
MATR_RIGI=MAS_RI_M,
MATR_RIGI_GEOM=MAS_RI_G,
OPTION='BANDE',
TYPE_RESU='MODE_FLAMB')
break
座屈モードを表示するために、高次要素を使って求めた結果を線形要素のモデルに投影します。
MODELIN = PROJ_CHAMP(identifier='42:1',
MAILLAGE_1=MAIL,
MAILLAGE_2=MA,
RESULTAT=RESULT0)
結果をファイルに出力します。
IMPR_RESU(identifier='43:1',
FORMAT='MED',
INFO=2,
RESU=(_F(MAILLAGE=MA,
RESULTAT=MODELIN,
TOUT='OUI')),
UNITE=80)
固有値の検索結果も出力しました。
IMPR_TABLE(TABLE=NBMOD1,
UNITE=8)
FIN()
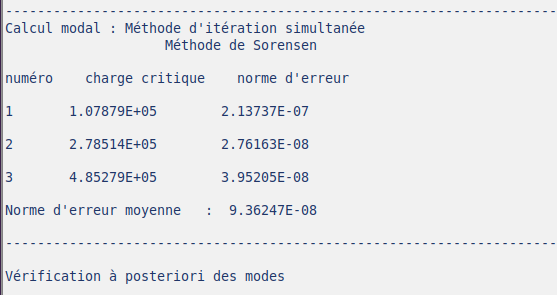
結果です。
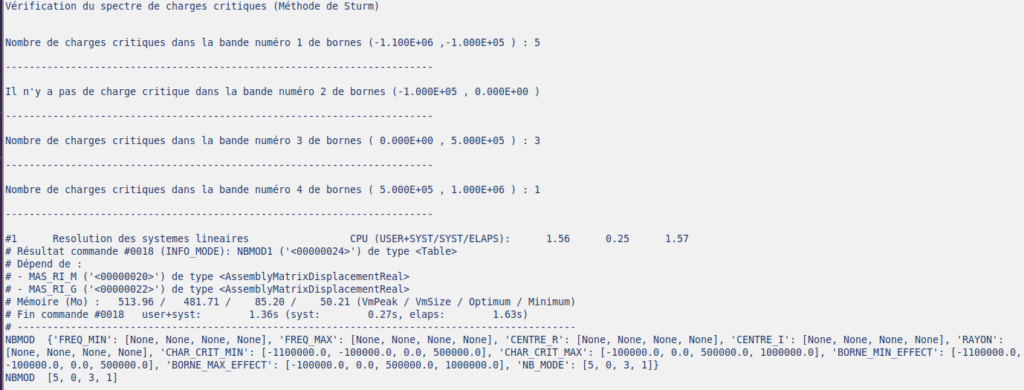
INFO_MODESの結果はちゃんと取り出せているようです。
そして、狙いどおりに固有値を計算してくれました。

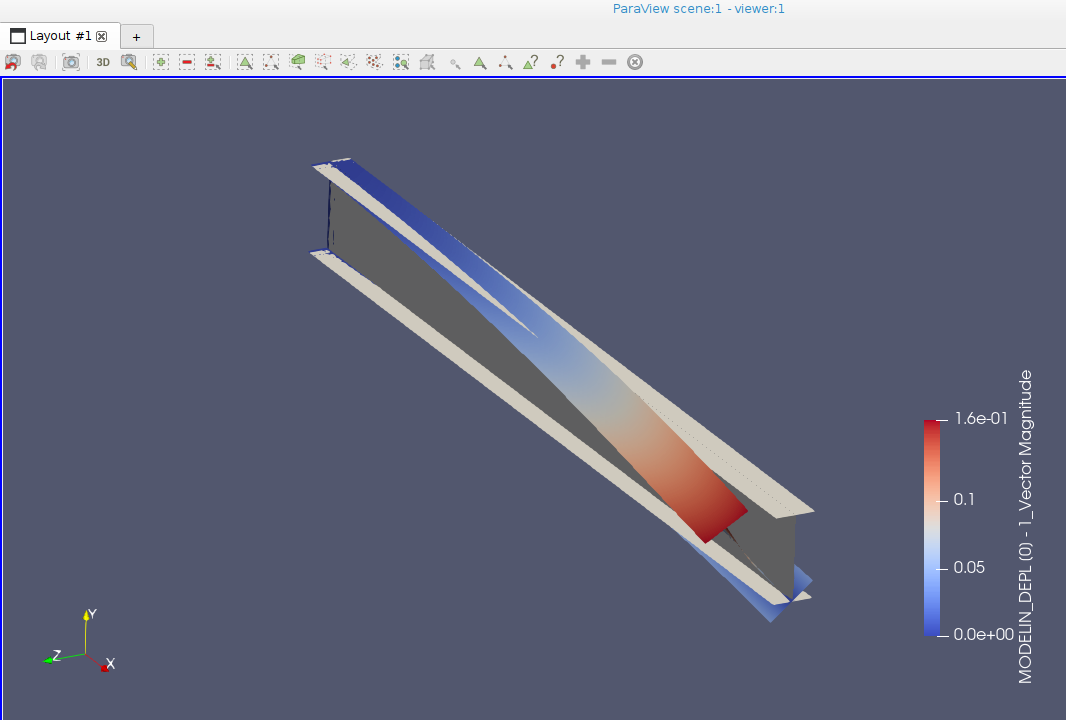
第1モードはこのようになりました。
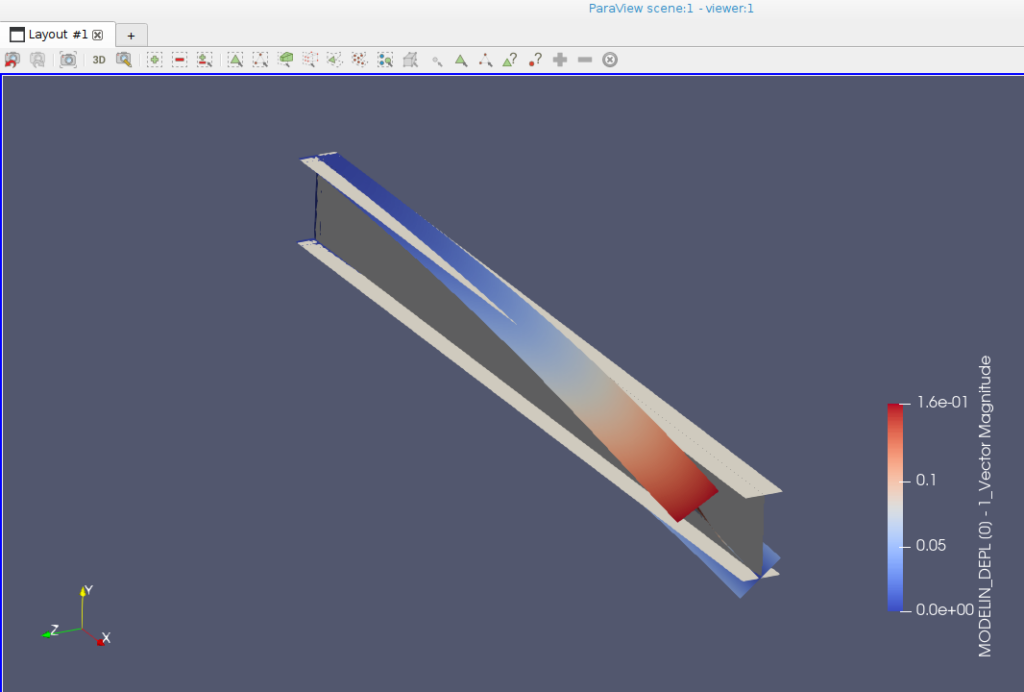
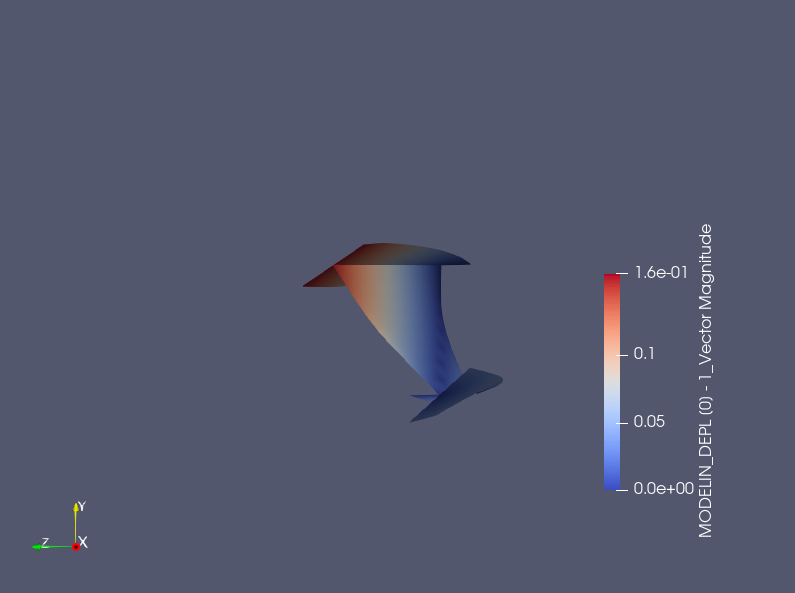
横に倒れていました。
応用です。INFO_MODE⇒CALC_MODESをfor文で繰り返して、0以上で最小の固有値を探します。
bands = [0.0,0.0]
for i in range(0,10): # from 0 to 1000000.0
bands[0] = 100000.0*float(i)
bands[1] = 100000.0*float(i+1)
NBMOD1 = INFO_MODE(CHAR_CRIT= bands,
COMPTAGE=_F(METHODE='STURM'),
MATR_RIGI=MAS_RI_M,
MATR_RIGI_GEOM=MAS_RI_G,
SOLVEUR=_F(METHODE='MUMPS'),
TYPE_MODE='MODE_FLAMB')
nbmod = NBMOD1.EXTR_TABLE()
nb_mode = nbmod.values()['NB_MODE']
if nb_mode[0] > 0:
RESULT0 = CALC_MODES(CALC_CHAR_CRIT=_F(CHAR_CRIT=(bands[0], bands[1]),
),
MATR_RIGI=MAS_RI_M,
MATR_RIGI_GEOM=MAS_RI_G,
OPTION='BANDE',
TYPE_RESU='MODE_FLAMB')
break
計算結果(mesu)を見てみると、目的の固有値を得ることができました。
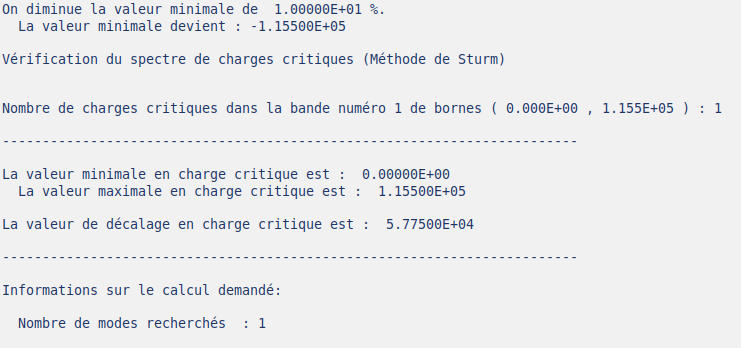
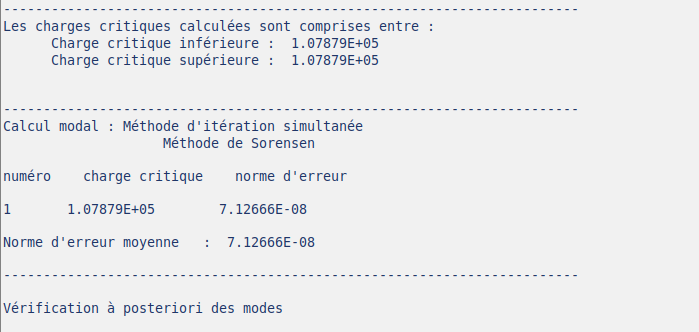
お疲れさまでした。
コメント