半球と平板の接触について解析しました。
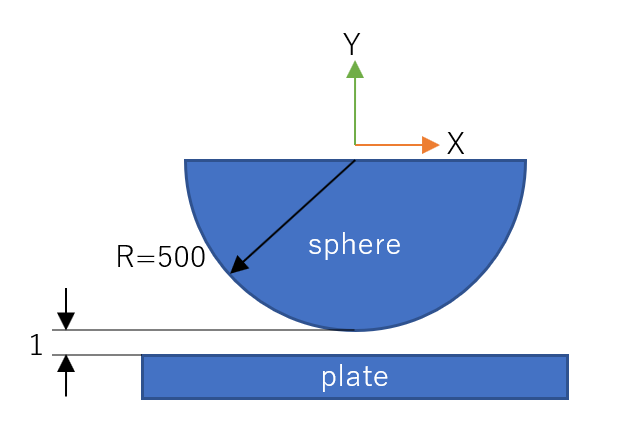
半径500mmの球を平板から1㎜の隙間を設けて配置しました。
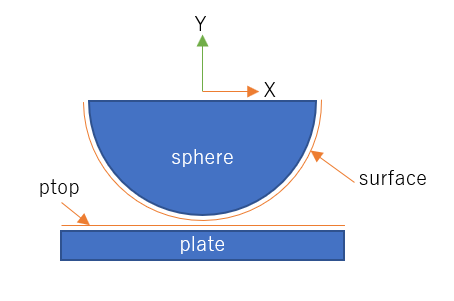
半球sphereと平板plateはsolid要素でモデル化します。そして接触の設定のため、各々の表面の2D要素を”surface”、”ptop”でgroup化します。
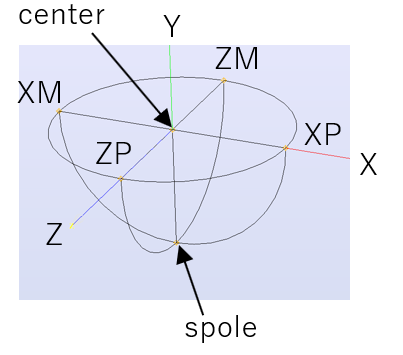
centerは荷重の作用点
XM、XP、ZM、ZPは仮想ばねを取り付ける節点
spoleは作用力を確認するための節点
commです。
まずは、いつもの開始の宣言です。messageは英語になるように”LANG=’EN’ “を追加しました。
DEBUT(identifier='0:1',
LANG='EN')
半球のmeshを読み込みます。
mesh = LIRE_MAILLAGE(identifier='1:1',
UNITE=20)
半球は拘束しない(できないので、このままでは荷重を加えたときに、変位が無限大になってしまいます。これを防ぐために、弱い仮想ばねを4か所に追加します。
newmesh = CREA_MAILLAGE(identifier='2:1',
CREA_POI1=_F(GROUP_NO=('XM', 'ZM', 'ZP', 'XP'),
NOM_GROUP_MA=('spElmt', )),
MAILLAGE=mesh)
仮想ばねを追加したmesh名は”newmesh”となりました。次に平板のmeshを読み込みます。
meshp = LIRE_MAILLAGE(identifier='3:1',
UNITE=2)
“newmesh”と”meshp”をまとめてmesh0とします。
mesh0 = ASSE_MAILLAGE(identifier='4:1',
MAILLAGE_1=newmesh,
MAILLAGE_2=meshp,
OPERATION='SUPERPOSE')
meshからmodelを設定します。。全体(solid要素)は3Dの力学現象です。ここで、仮想ばねの要素を”DIS_T”とします
model = AFFE_MODELE(identifier='5:1',
AFFE=(_F(MODELISATION='3D',
PHENOMENE='MECANIQUE',
TOUT='OUI'),
_F(GROUP_MA=('spElmt', ),
MODELISATION='DIS_T',
PHENOMENE='MECANIQUE')),
MAILLAGE=mesh0)
仮想ばねの剛性を設定します。今回はX、Y、Z方向ともに50N/mmとしました。
softSp = AFFE_CARA_ELEM(identifier='6:1',
DISCRET=_F(CARA='K_T_D_N',
GROUP_MA=('spElmt', ),
VALE=(50.0, 50.0, 50.0)),
MODELE=model)
材料は鋼です。
steel = DEFI_MATERIAU(identifier='7:1',
ELAS=_F(E=206800.0,
NU=0.29))
設定した材料を、modelに適用させます。
fieldmat = AFFE_MATERIAU(identifier='8:1',
AFFE=_F(MATER=(steel, ),
TOUT='OUI'),
MODELE=model)
今回、荷重は少しづつ加えていきます。そのためのstepを刻む関数を定義します。0から1までを50分割しました。
listr = DEFI_LIST_REEL(identifier='9:1',
DEBUT=0.0,
INTERVALLE=_F(JUSQU_A=1.0,
NOMBRE=50))
stepと荷重の関係を示す関数です。今回は、シンプルに線形です。
func = DEFI_FONCTION(identifier='10:1',
NOM_PARA='INST',
VALE=(0.0, 0.0, 1.0, 1.0))
拘束条件と荷重を設定します。半球に1000N加えたいのですが、仮想ばねが4本×1mm(隙間)×50N/mm=200N受け持つので、1200Nと設定します。
load = AFFE_CHAR_MECA(identifier='11:1',
FORCE_NODALE=_F(FY=-1200.0,
GROUP_NO=('CENTER', )),
MODELE=model)
fix = AFFE_CHAR_MECA(identifier='12:1',
DDL_IMPO=_F(DX=0.0,
DY=0.0,
DZ=0.0,
GROUP_NO=('nbottom', )),
MODELE=model)
接触を設定します。今回は摩擦は無しです。
contact = DEFI_CONTACT(identifier='13:1',
ALGO_RESO_CONT='NEWTON',
ALGO_RESO_GEOM='NEWTON',
FORMULATION='CONTINUE',
LISSAGE='OUI',
MODELE=model,
ZONE=_F(ALGO_CONT='STANDARD',
APPARIEMENT='MAIT_ESCL',
CONTACT_INIT='OUI',
GROUP_MA_ESCL=('surface', ),
GROUP_MA_MAIT=('ptop', )))
初期隙間が大きすぎたようで、初回の計算が収束しなかったので、”CONTACT_INIT=OUI”を追加しています。
非線形解析の設定です。
resnonl = STAT_NON_LINE(identifier='14:1',
CARA_ELEM=softSp,
CHAM_MATER=fieldmat,
CONTACT=contact,
CONVERGENCE=_F(ITER_GLOB_ELAS=50,
ITER_GLOB_MAXI=50),
EXCIT=(_F(CHARGE=load,
FONC_MULT=func),
_F(CHARGE=fix)),
INCREMENT=_F(LIST_INST=listr),
METHODE='NEWTON',
MODELE=model)
計算結果から、Mises応力と節点力を求めるように設定します。
resnonl = CALC_CHAMP(identifier='15:1',
reuse=resnonl,
CONTRAINTE=('SIGM_NOEU', ),
CRITERES=('SIEQ_NOEU', ),
DEFORMATION=('EPSI_NOEU', ),
FORCE=('FORC_NODA', ),
RESULTAT=resnonl)
節点力を表形式で出力するための設定です。
table = POST_RELEVE_T(identifier='16:1',
ACTION=_F(GROUP_NO=('SPOLE', ),
INTITULE='SPC',
NOM_CHAM='FORC_NODA',
OPERATION=('EXTRACTION', ),
RESULTANTE=('DX', 'DY', 'DZ'),
RESULTAT=resnonl,
TOUT_ORDRE='OUI'))
変位と応力の出力を設定します。
IMPR_RESU(identifier='17:1',
RESU=_F(RESULTAT=resnonl,
TOUT='OUI'),
UNITE=80)
節点力の出力を設定します。
IMPR_TABLE(identifier='18:1',
TABLE=table,
UNITE=8)
FIN(identifier='19:1',
結果です。
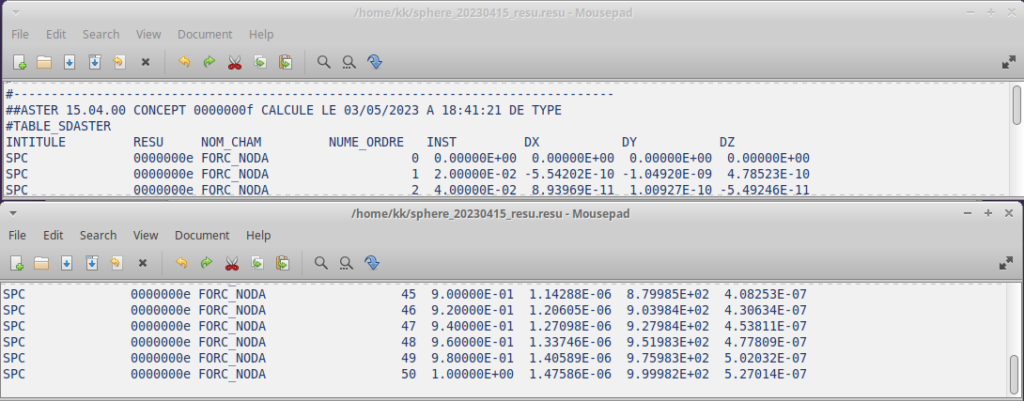
節点spoleへの作用力は予定どおり。
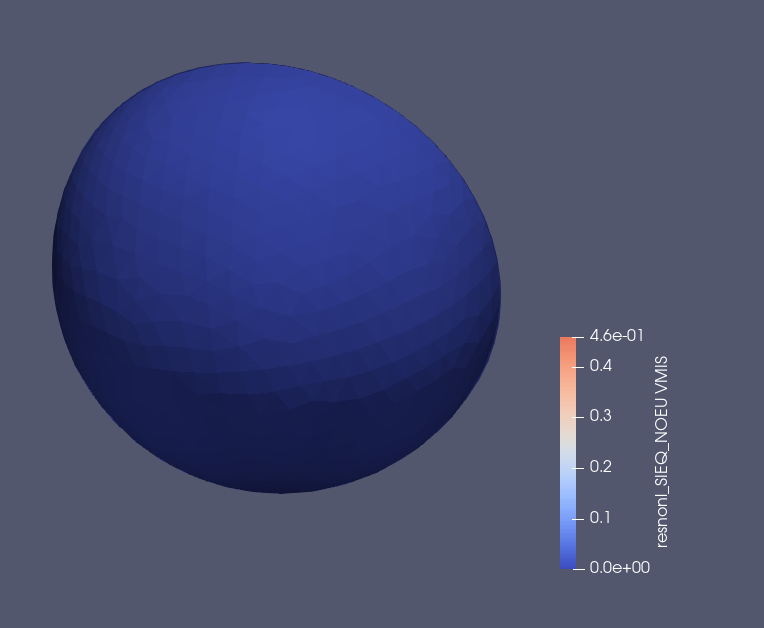
変位はこんな感じ。倍率は10です。



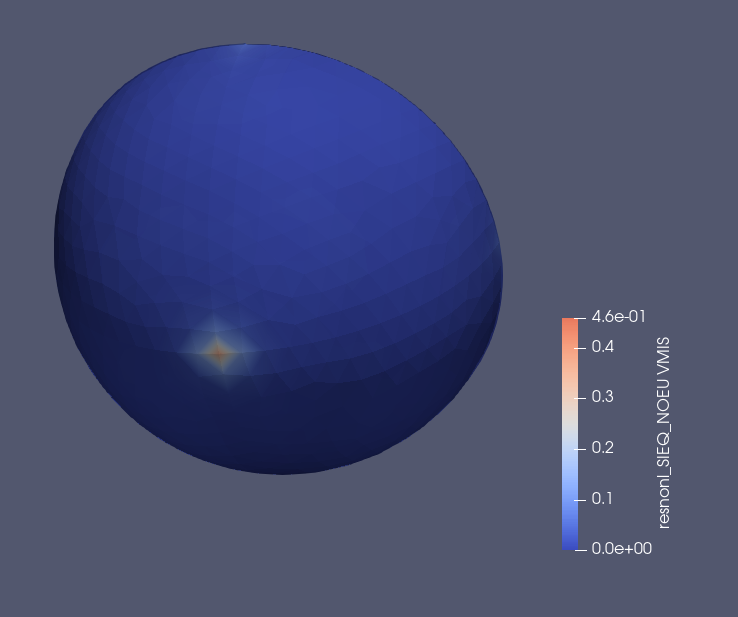
接触部のMises応力
コメント